暦Wiki
角運動量とその保存†
角運動量 (angular momentum)†
- 物体の位置 r と運動量 p の外積 L = r×p を角運動量と呼びます。
- 外積の特徴から、角運動量は位置ベクトルr と運動量ベクトル p の作る平面に対して垂直で、その大きさは r と p の作る平行四辺形の面積に等しいことがわかります。
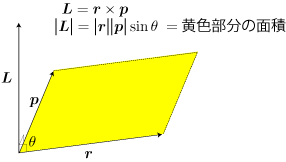
- 運動を直角方向に変換する量、すなわち、物体の回転運動を表すのに適しています。
- 右手の4本の指を回転方向にそろえると、親指の方向が角運動量ベクトルの方向を表わします。
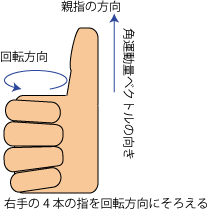
角運動量の保存†
- 角運動量の単位時間当たりの変化量は、

- r × F をトルクといいます。
- 外部から力が加わらない場合、または力 F が位置ベクトル r に平行な場合は r × F=0となり、角運動量は変化しないことがわかります。これを角運動量保存則といいます。
- 万有引力の法則のような力は位置ベクトル r に平行に働きますから、角運動量が保存される典型的な例になります。
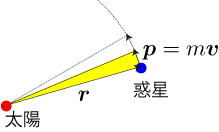
- 短い時間の間に惑星と太陽を結ぶ線は下図の黄色のような図形を描きます。
- 単位時間当たりの面積増加量は1/2|r×v|=|r×p|/2m=|L|/2mとなりますが、角運動量保存則によりこの値は常に一定です。
- したがって、惑星と太陽を結ぶ線が一定時間に描く面積は常に等しい、すなわちケプラーの第2法則が成り立ちます。

- 角運動量は公転だけではなく、自転すなわち自分自身を軸とする回転でも定義できます。
たとえば、スケート選手が手を縮めたり真上に伸ばしたりすると回転が速くなり、手を横に広げると回転が遅くなるのも、角運動量が保存されるために起こる現象の例です。
- 手を縮める=rを小さくする→Lを一定にするために、pは大きくなる
- 手を広げる=rを大きくする→Lを一定にするために、pは小さくなる
関連ページ†
Last-modified: 2020-05-27 (水) 15:31:55




