暦Wiki
天体の形†
大きな天体は丸い†
- 小惑星や彗星には複雑な形をしたものがたくさんありますが、ある程度大きな天体になるとみんな丸い形をしています。
- 太陽のようにガスでできた天体も、地球のように岩石でできた天体も、どれも同じように丸くなります。
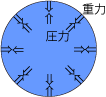
- これは、天体が大きく=重くなると、すべての物質がもつ引き合う力=万有引力も大きくなり、複雑な形を保つことが難しくなるためです。
- 最終的には自らの引力によってつぶれようとする力と内部の物質が反発しあう圧力とが拮抗しあい、丸い形になって安定します。
自転する天体は横に膨らむ†
- これに自転による遠心力が加わると、天体は赤道方向に膨らみます。
- 遠心力の大きさは自転軸からの距離に比例しますから、赤道上で最も大きく、北極や南極では0になります。そのため赤道方向に伸ばされるわけです。
- 天体は常に自転していますから、この遠心力を加えた状態で安定な形を保とうとします。
- このような赤道方向が長い、楕円を回転させたような形を回転楕円体といいます。
- 赤道方向に測った半径を赤道半径(a)、極方向に測った半径を極半径(b)、この回転楕円体と体積が同じになるような球の半径を平均半径(r)といいます。すなわち、r3=a2bです。
- 赤道半径と極半径の差を赤道半径で割ったものを扁平率(f)といい、回転楕円体の膨らみ具合を表します。すなわち、f=(a−b)÷aです。

- 地球も完全な球ではなく、北極方向よりも赤道方向が長い形をしています。
- 自転の速い天体ではより極端に膨らんだ形状になります。
潮汐は天体を引き伸ばす†
- 潮汐作用により、天体は力を及ぼす天体の方向とその反対方向に引き伸ばされます。
- 潮汐による変形は摩擦を伴い、次第に自転速度が減少していきます。
- 究極的には自転と公転が同期して、中心星に対して常に同じ面を向けるようになります。
- そのような状態では常に同じ方向に引き伸ばされることになりますから、潮汐力も加えた状態で安定な形を保つようになります。
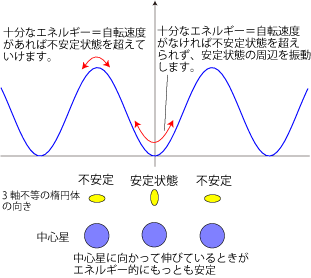
- すなわち、中心星の方向とその逆方向に伸びた、3軸不等の楕円体です。
- 逆に、質量分布が特定の方向に偏っているなど、もともと3軸不等の楕円体である場合には、その方向と中心星の方向がそろうときが安定です。
- 究極的には形によって決まる方向で、自転と公転が同期することになるでしょう。
- ただし、こちらにはエネルギーを失い自転を減速させる効果はありませんので、自転速度が速ければ意味がありません。
- つまり、最初は潮汐摩擦により減速しつつ、最終的には潮汐と形状の両者が互いに影響しあって安定する方向・形が決まることになります。
- 最終的な安定状態になる前に天体が固まり、途中の準安定状態を反映した形状になってしまうこともあります。
- 地球のような同期状態にない天体は潮汐により伸びる方向が常に変化していきます。
- しかし、地球上の位置〜緯度、潮汐作用を及ぼす天体の位置〜赤緯の関係は均等ではありませんので、平均をとっても影響は0になりません。これを永年潮汐力といいます。
- その結果、地球は永年潮汐力を加えた状態で安定な形となります。永年潮汐力による変形量を永年変形といいます。
- 永年変形は氷河の後退など他の要因による変形と区別することは困難です。
- このため、潮汐の扱いには3通りの考え方があります。
- 永年潮汐力を含めた、実際の平均値に近い体系をmean tide systemといいます。
- 永年潮汐力は除きますが、永年変形は無理に取り除かずそのまま残した体系をzero-frequency tide systemまたはzero tide systemといいます。
- 仮定を設けて永年変形も取り除き、潮汐の影響をすべて排除した体系をtide-free systemまたはnon-tidal systemといいます。
関連ページ†
Last-modified: 2020-05-27 (水) 18:49:17


