暦Wiki
太陽年と二至二分†
- 直観的には、春分から次の春分まで/秋分から次の秋分までといった二至二分の間隔を測れば、1太陽年の長さは求まるように思えます。
- しかし、話はそう簡単ではありません。
二至二分の間隔†
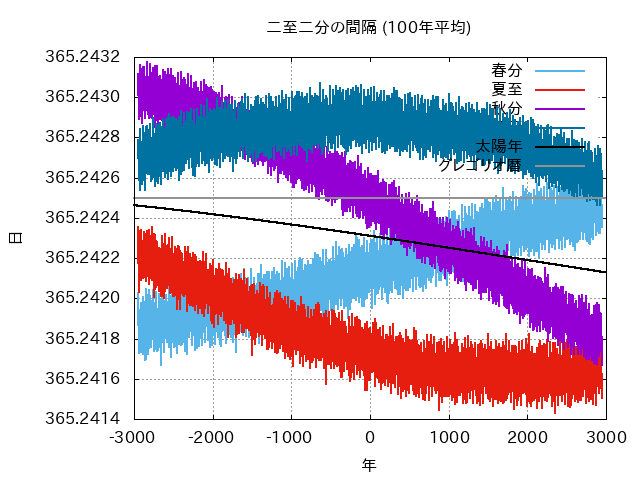
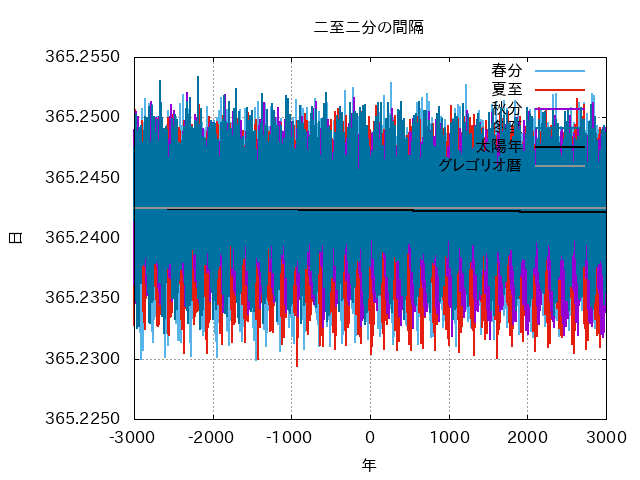
- 二至二分の間隔には±15分程度のばらつきがあり、しかも複雑に変動します。
- このばらつきは惑星・月・章動・楕円軌道の影響による本質的なものであり、どんなに精度よく観測できても消えることはありません。
- 周期の異なる、大きなばらつきが含まれるため、数年観測を続けて値を平均しても、なかなか収束してくれません。
- 寛政暦以前のように改暦前にちょっと観測する程度では、そんなにずれていないという確認がせいぜいでしょう。
- それぞれの影響を正確に見積もることができれば理論的に除くことも可能*1ですが、見積もりが不十分ではどうにもなりません。
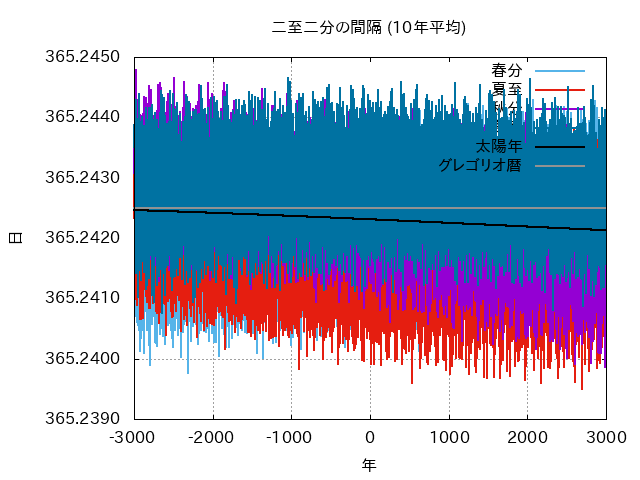
- 周期がわかっていれば、それを利用してばらつきを抑えることも、ある程度は可能です。
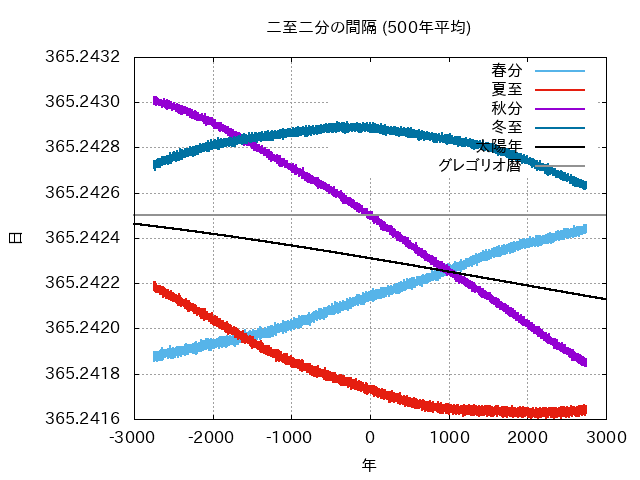
- たとえば、章動の主要項は18.6年周期ですから、それに近い19年やその5倍の93年の平均値なら、だいぶ見通しがよくなります。
- といっても、章動が発見されたのは18世紀のことですし、そのようなデータが都合よくあるとも限りません。
- また、すべてを完全に打ち消すことは困難でしょう。
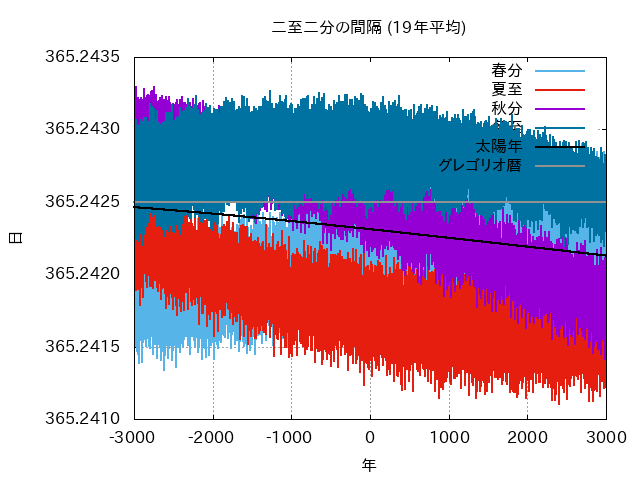
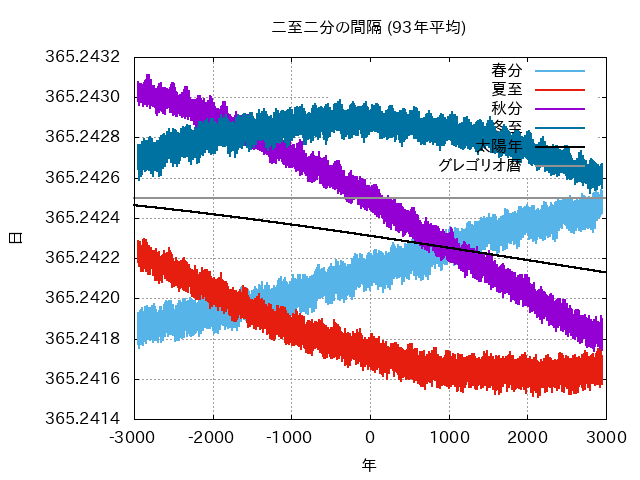
- たとえ見積もりが正確にできなくても、十分長い期間で平均すれば、とりあえず収束はします。
太陽年の長さは求まるのか?†
- バランスよくデータを取得できれば、平均値が1太陽年の長さに近い値となる可能性もあります。
- しかし、冬至や夏至に比べて春秋分は精度よく観測できますから、どうしても観測データは春秋分に偏りがちです。
- バランスが良いか評価するのも、限られたデータでは困難でしょう。
- 楕円軌道の影響は歳差と近日点の移動に伴い変動しますから、太陽年の値も時間変動します。
- 1000年程度なら変動は概ね単調ですので、平均値は平均した期間の中央における値とみなせます。逆に言えば、観測時点での平均値は得られません。
- 時間変動の評価にはより長期にわたるデータが必要となります。
- 仮にデータがあっても春分に偏っていれば、時間とともに増加という太陽年とは真逆の挙動にもなりえます。
- 長期間になれば地球の自転変動も無視できなくなり、評価はさらに困難となります。
- 結局、
- 単純に二至二分の平均間隔を求めるというやり方では、365.242日〜分単位くらいがせいぜいでしょう。
- それでも、太陽年の長さの概略値としては十分であり、18世紀ごろまでは実際そのように扱われました。
- 秒単位以上の精度で値を得るには、各影響の大きさを見積もって補正することが不可欠となります。
- 幸い、歳差と近日点の移動により、西暦1000年前後は春秋分の間隔が太陽年に近いフェーズにありました。この期間なら、補正の必要性は低くなります。
関連ページ†
Last-modified: 2022-07-06 (水) 16:46:46