暦Wiki
月離/月行遅疾†
- 日本や中国で使われていた太陰太陽暦では、月の運動を月離、月の動きが速くなったり遅くなったりすることを月行遅疾といいます。
- 前漢のころまでの渾天儀には黄道環がなく、赤道を基準に観測していました。
- 仮に太陽が黄道上を一定の速さで動いていったとしても、赤道方向に換算した動きは赤道と黄道の傾きにより変化します。
- 甘露二年(紀元前52年)の耿寿昌による報告から、そのようなみかけの変動が実際に観測から得られていたことがわかります。
- 後漢に入ると、傅安が黄道を基準に太陽や月の運行を観測します。
- 永元四年(92年)賈逵は、黄道による観測の優位性、さらには見かけ上でない真の月行遅疾の存在について論じています。
- 黄道を基準に観測すれば見かけ上の遅疾は起こらず、予測が正確になる。
- 朔・弦・望・月食の時刻予測が的中しないのは今の史官が真の月行遅疾を理解していないため。
- 李梵と蘇統によれば、月行遅疾は特定の宿で起こるのではなく、速く動くところは1朔望月で3度移動し、9年で一回りする。
- これは近地点が1朔望月に約3度、8.85年で一回りすることを表わしています。
- 後漢末の劉洪による乾象暦 *1で、月行遅疾も採り入れられることになりました。
- 定朔が採用されるのは唐の時代になってからのことです。
- 定朔とは、月の満ち欠けを平均値でなく実際の月の満ち欠けを用いて決める方法です。
- 定朔を導入すると、大の月や小の月が連続して現れるようになります。このため、元嘉暦を作った何承天も定朔を提案しましたが、受け入れられませんでした。
- その後、隋の劉焯による皇極暦では日行盈縮も採り入れられ、ようやく唐の戊寅暦において定朔が導入されることになりました。日本では儀鳳暦からということになります。
- それでも、大の月が4回続く四大を避けるため平朔に戻されたり、夕方以降に朔となる場合は朔を翌日にする進朔が行なわれたりといった調整が続きました。
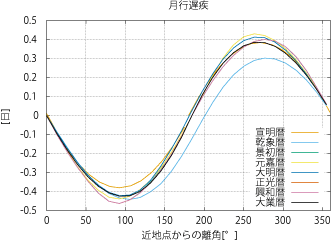
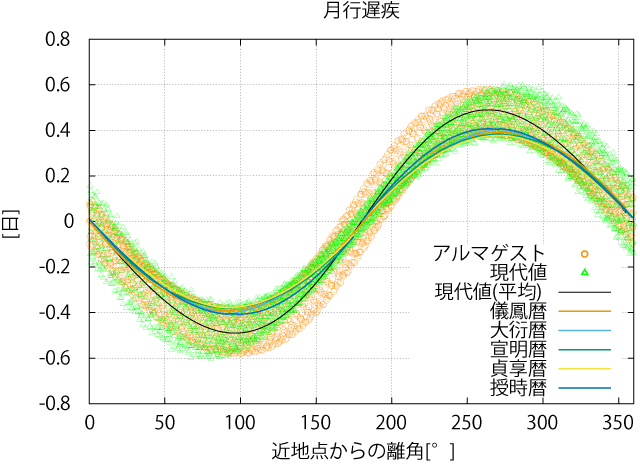
- 宝暦暦までの月行遅疾は、どれも似たような値をとります。
- 現代値(平均)の示すカーブよりも浅いカーブになります。
- これに対し、アルマゲストは現代値(平均)の周りに分布します。
- これはアルマゲストが出差を考慮しているのに対し、これらの暦がそれを考慮していないためです。
- 中心差をA、出差をB、月と太陽の黄経差をD、月の平均近点角をlとすると、月の真近点角fはf≒l+A sin l+B sin(2D−l) と書けます。
- 月行遅疾Δは平均からのズレのことであり、Δ=f−l≒A sin l+B sin(2D−l) です。
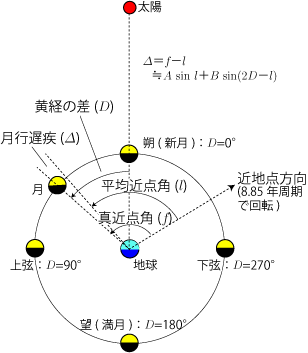
- この月行遅疾Δは、
- 朔(D=0°)や望(D=180°)のときには、Δ=(A−B) sin l になります。
- 上弦(D=90°)や下弦(D=270°)のときには、Δ=(A+B) sin l になります。
- したがって、朔や望だけを考えるのであれば、Δ=A sin l よりも、Δ=(A−B) sin l の方が現実にあうことになります。
- 理科年表によれば、A〜6.29°、B〜1.27°であり、l=90°, 270°といったピーク付近では平均速度v〜13.176°/日に近いですから、月行遅疾のピーク値はA÷v〜0.48日、(A−B)÷v〜0.38日となります。
- つまり、これらの暦の月行遅疾はΔ=(A−B) sin l に準じて定められているだけで、朔や望の推算に使う分にはそれほど悪くない値といえるでしょう。
- さらに、現代値の分布を見ると、近地点(l=0°)付近よりも遠地点(l=180°)付近の方が変動が小さいこともわかります。
- これは二均差の影響であり、アルマゲストでも考慮されておりません。
- 宣明暦などでは遠地点を基準に近点月の長さを決めていますが、これは理にかなっているといえるでしょう。
- ケプラーの楕円運動など近代の西洋天文学を採り入れた寛政暦や天保暦では現代値とほぼ同じになります。

関連ページ†
- 参考
- 国立天文台編「理科年表平成28年版」, 丸善(2015).
- 後漢書志第ニ 律暦中
ただし、採用されたのは呉の黄武二年(223年)になってから。->
本文(1)に戻るLast-modified: 2021-08-11 (水) 15:35:43