暦Wiki/アルマゲスト - 国立天文台暦計算室

アルマゲスト (Almagest)†

アルマゲストは2世紀ごろプトレマイオスによってまとめられた古代天文学の集大成ともいえる書物です。
地球を中心とした天体の運動＝天動説のバイブル的存在で、離心円、周転円などの概念を用いて太陽・月・惑星などの運動を論じています。

離心円 (Eccentric circle)†

季節の長さ†

春分・夏至・秋分・冬至の間隔が等しくないことは既に知られていました。
- ヒッパルコスによれば、春分から夏至までは94日12時間、夏至から秋分までは92日12時間、秋分から冬至までは88日3時間、冬至から春分までは90日3時間かかります。
  - ヒッパルコスは赤道環のような装置を用いて観測していたようです。
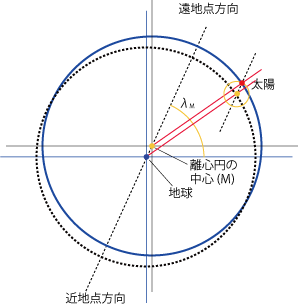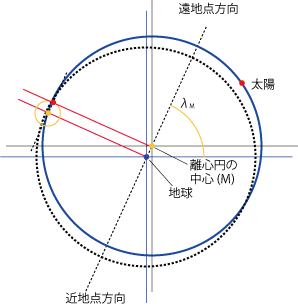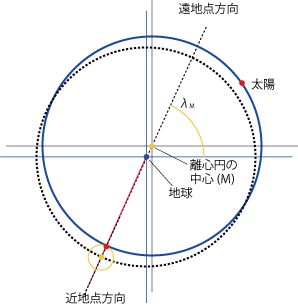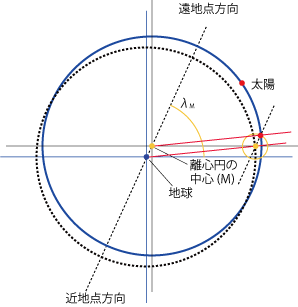
- そこで、太陽は地球を中心とした円ではなく、地球とは異なる点を中心とした円＝離心円の上を等速で円運動していると考えます。
地球から見て春分・夏至・秋分の方向はそれぞれ90°間隔ですが、離心円の中心(M)から見た角度はそれとは異なります。
- 太陽は離心円上を等速で運動しますから、公転速度ω＝360°÷365.25日です。Mから見た角度はこれに所要日数をかけて、春分と夏至のなす角度は93.142°、夏至と秋分のなす角度は91.170°となります。
- Mから見た春分と秋分の方向のズレδ₁は等しいので、180°＋2δ₁＝93.142°＋91.170°。したがって、δ₁＝2.156°
- 夏至の方向のズレδ₂は図より、δ₁＋90°＋δ₂＝93.142°。したがって、δ₂＝0.986°
- そのほかの季節で検算すると、
  - 秋分から冬至は(90°－δ₁－δ₂)÷ω＝88日3時間
  - 冬至から春分は(90°－δ₁＋δ₂)÷ω＝90日3時間

離心円の中心(M)の位置†

地球とMのズレ(x,y)は離心円の半径をRとすると、x＝R sinδ₂、y＝R sinδ₁であり、
- 方向λ_M＝arctan(y/x)≒65.42°
- 距離Re＝sqrt(x^2+y^2)≒0.04137R
なお、上記では小数演算や三角関数など若干の簡略化をしております。アルマゲストでは60進法などを用いて、
- 1年の長さは365.25日より1/300日短い＝365;14,48日*1としているので、太陽の公転速度は360°÷365;14,48日≒0;59;8,17,13,12,31°/日
- 方向λ_Mは65;30°、距離ReはR=60とすれば2;30、すなわちe＝1/24という値を導き出しています。

離心円の役割†

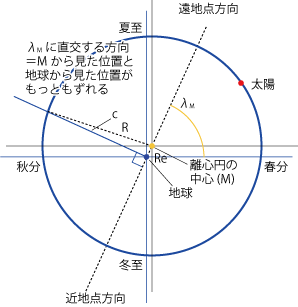
λ_Mは太陽が地球からもっとも遠ざかる方向＝遠地点(遠日点)、その逆は太陽が地球にもっとも近づく方向＝近地点(近日点)です。
- 地球の近日点黄経ϖが65.42°くらいになるのは紀元前180年ごろですので、ヒッパルコスの成果としてはよい数値といえるでしょう。
λ_Mと直交する方向に太陽が来るとき、Mから見た位置と地球から見た位置がもっとも大きくずれます。
- ズレの大きさcは sin c ＝ Re / R ＝ eより、c≒2.37°です。
- 地球の離心率から導かれる値は1.9°ですので、若干大きいですがまぁよい数値といえるでしょう。
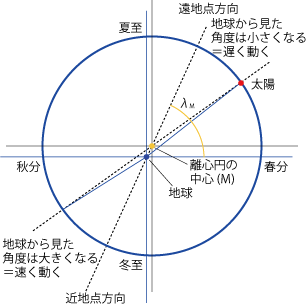
太陽が一定時間に動く角度はMから見れば等しくなりますが、地球から見た場合は角度が変化します。
- 近地点付近では地球から見た角度は大きくなる＝速く動くように見えます。
- 遠地点付近では地球から見た角度は小さくなる＝遅く動くように見えます。
- このように、ケプラーの第2法則とも定性的には合致していることがわかります。
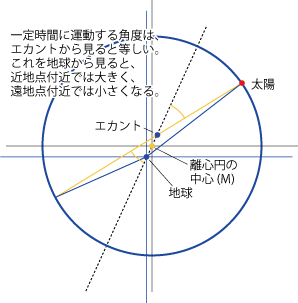
このように、離心円は楕円軌道に相当する役割を持っています。
- さらに、離心円上の運動を、離心円の中心Mに対してではなく、Mをはさんで地球のちょうど反対側にある点に対して一様に運動すると仮定すれば、よりよい精度で楕円運動を近似することができます。
- この、Mをはさんで地球のちょうど反対側にある点のことをエカント (Equant) と呼びます。

周転円 (Epicycle)†

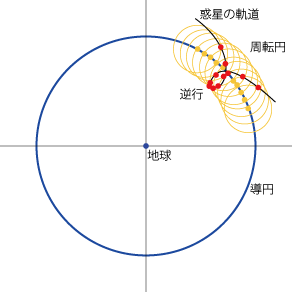
惑星や月の運動を表現するにはより複雑なモデルが必要になります。
- そこで使われるのが円運動する点の周りを円運動するというモデルです。最初の円を導円 (Deferent)、導円上の点を中心とする円を周転円 (Epicycle) といいます。
- 惑星の逆行などもこれで再現できます。

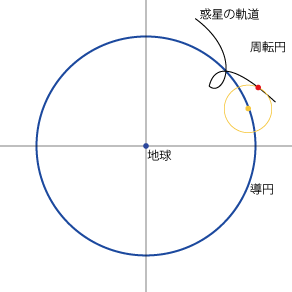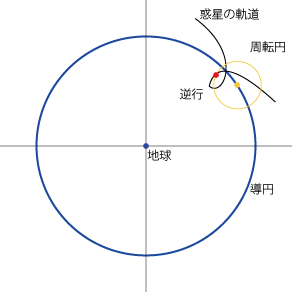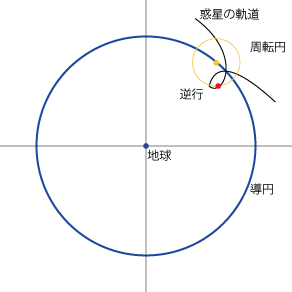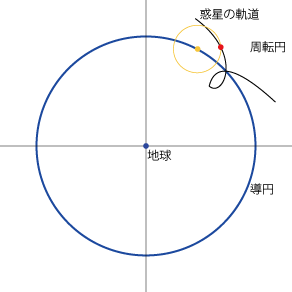
周転円の役割†

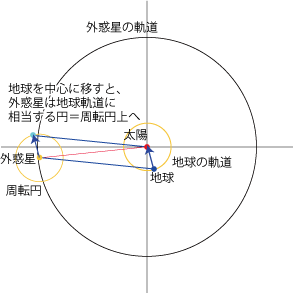
太陽の周りを地球と外惑星がそれぞれの公転周期で等速円運動しているとします。簡略化はしていますが、いわゆる地動説です。
- この図で地球を中心に考える＝地球を太陽の位置に移すと、外惑星は地球の軌道に相当する円上にスライドします。これが周転円になります。
- つまり、導円は外惑星本来の運動を、周転円は地球の運動を表わすものであり、これらを合成したものが地球から見た外惑星の動きとなるわけです。
  - 地球→周転円中心の方向＝太陽→外惑星の方向
  - 周転円中心→外惑星の方向＝地球→太陽の方向：方向は惑星によらず、1年周期で変動します。
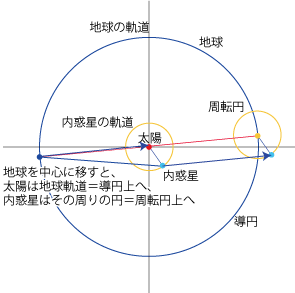
同様に、太陽の周りを地球と内惑星がそれぞれの公転周期で等速円運動しているとします。
- この図で地球を中心に考える＝地球を太陽の位置に移すと、太陽は地球の軌道に相当する円上にスライドし、内惑星はその周りの円上に移動します。これが周転円になります。
- つまり、導円は地球の運動を、周転円は内惑星の運動を表わすものであり、これらを合成したものが地球から見た内惑星の動きとなるわけです。
  - 地球→周転円中心の方向＝地球→太陽の方向：惑星によらず、太陽とともに動きます。
  - 周転円中心→内惑星の方向＝太陽→内惑星の方向
  - 太陽から大きく離れることはなく、その前後を行き来します。
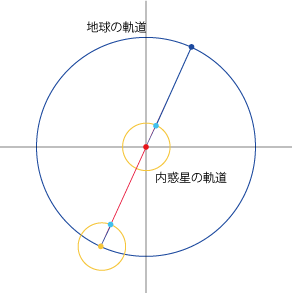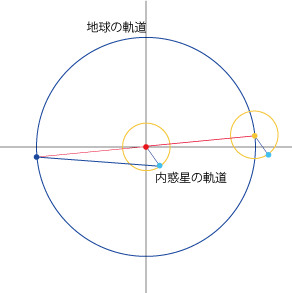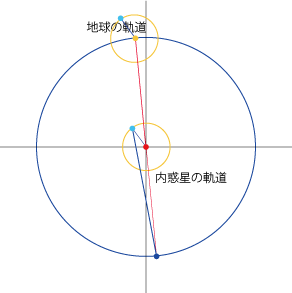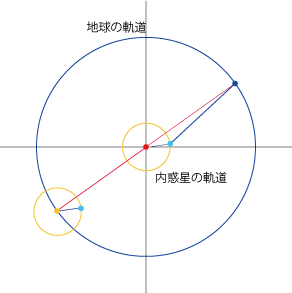
つまり、周転円を使うことで惑星と地球の運動を分離し、さらに離心円やエカントも導入して、惑星の楕円運動を精密に再現したわけです。
このように、惑星が周転円上を運動することと、惑星・地球がともに太陽の周りを公転することは、視点が異なるだけでまったく同じことを表わしています。
- 実際、暦象年表や理科年表に掲載される惑星の位置を図にしても、このような周転円状の動きが得られます (理科年表オフィシャルサイト )。
- しかし、プトレマイオスの理論が観測精度に比べて十分精密であったことに加え、地球を世界の中心とする宗教的概念による制約もあり、視点を変えるという発想は困難なものとなっていきました。
- そんな状況を打破したのが16世紀の天文学者コペルニクスです。そこで、このような発想の大転換をコペルニクス的転回と呼んでいます。

周転円と離心円†

以下の2つはまったく同じ運動を表わしています。
- 地球から距離Reだけ離れた点を中心とする半径Rの円＝離心円上を速さωで反時計回りに運動する点の動き
- 地球を中心とした半径Rの導円上を速さωで反時計回りに運動する点Cがあり、Cを中心とする半径Reの周転円上を、遠地点方向＝地球とCを結ぶ方向に対して速さωで時計回りに運動する点の動き
つまり、離心円は周転円の特殊ケースと見ることもできます。
- 月の場合は地球の動きを表わす周転円は不要ともいえますが、周転円を使うことで一般化し、さらに複数の周期を表現することができます。

出差†

周転円モデルによって日食や月食を予報することは可能になりました。
- 日食や月食では月と太陽が同じあるいは真逆な方向に来ますので、太陽の位置から月の位置がわかります。
- とくに月食は視差の影響を受けませんので、月食を用いて周転円半径などのモデルパラメータを推定することができます。
しかし、そのようにして得たモデルで月の位置を予測しても、日月食以外では観測との間にズレがありました。
- 朔や望(新月や満月)ではズレは見られない。
- 上弦や下弦でも月が近地点や遠地点にいるときにはズレは小さい。
- 上弦や下弦で、月が近地点・遠地点方向と垂直な方向にあるときにもっとも大きくずれる。
- 楕円運動の影響＝中心差も加味されていますが、このズレが後に出差と呼ばれる月の不等です。
このような動きを実現するため、プトレマイオスは導円の中心を月と太陽の離角にあわせて回転させるというモデルをさらに追加しました。
- 導円の中心は朔のときに太陽と地球の間にあり、月の満ち欠け周期で時計回りに回転します。
- これにより月の方向はより正確に予測できるようになりましたが、地球と周転円の距離を無理やり変えるモデルだったため、月の距離についてはむしろ現実的でないものになってしまいました。
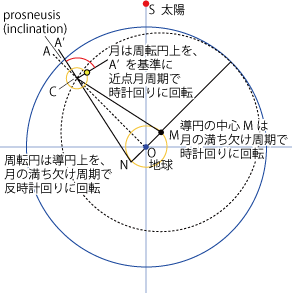
周転円内の運動は遠地点方向を基準としますが、このモデルでは遠地点方向がどこか不明瞭です。
- プトレマイオスは地球を挟んで導円の中心Mと反対側にある点Nから周転円の中心Cを結ぶ方向A'を平均の遠地点方向としました。
- このA'と、地球と周転円の中心Cを結ぶ方向Aとのずれをprosneusis (inclination) といいます。
- prosneusisは月と太陽の離角が60°や120°のときにもっとも大きくなるものであり、45°でピークとなる二均差とは異なります。

星座†

現在も使われる88星座のうち、48星座がまとめられています。
- 現在では、アルゴ座はりゅうこつ座、とも座、ほ座に分割されています。

暦Wiki

アルマゲスト (Almagest)†

離心円 (Eccentric circle)†

季節の長さ†

離心円の中心(M)の位置†

離心円の役割†

周転円 (Epicycle)†

周転円の役割†

周転円と離心円†

出差†

星座†

関連ページ†